WEB DESK, July 20(ABC): Many of the most challenging optimization problems encountered in various disciplines of science and engineering, from biology and drug discovery [1] to routing and scheduling [2] can be reduced to NP-complete problems.
Intuitively speaking, NP-complete problems are “hard to solve” because the number of operations that must be performed in order to find the solution grows exponentially with the problem size. The ubiquity of NP-complete problems has led to the development of dedicated hardware (such as optical annealing and quantum annealing machines like “D-Wave”) and special algorithms (heuristic algorithms like simulated annealing).
Recently, there has been a growing interest in solving these hard combinatorial problems by designing optical machines. These optical machines consist of a set of optical transformations imparted to an optical signal, so that the optical signal will encode the solution to the problem after some amount of computation.
Such machines could benefit from the fundamental advantages of optical hardware integrated into silicon photonics, such as low-loss, parallel processing, optical passivity at low optical powers and robust scalability enabled by the development of fabrication processes by the industry.
However, the development of compact and fast photonic hardware with dedicated algorithms that optimally utilize the capability of this hardware, has been lacking. Today, the path to solving NP-complete problems with integrated photonics is open due to the work of Charles Roques-Carmes, Dr. Yichen Shen, Cristian Zanoci, Mihika Prabhu, Fadi Atieh, Dr. Li Jing, Dr. Tena Dubcek, Chenkai Mao, Miles Johnson, Prof. Vladimir Ceperic, Prof. Dirk Englund, Prof. John Joannopoulos, and Prof. Marin Soljacic from MIT and the Institute for Soldier Nanotechnologies, published in Nature Communications.
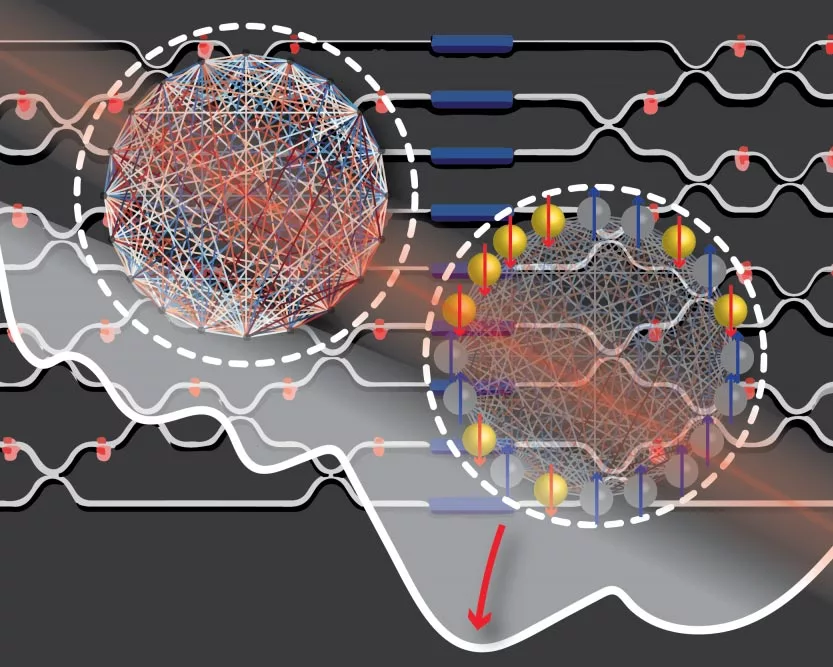
In this work, the MIT team developed an algorithm dedicated to solving the well-known NP-complete Ising problem with photonics hardware. Originally proposed to model magnetic systems, the Ising model describes a network of spins that can point only up or down.
Each spin’s energy depends on its interaction with neighboring spins — in a ferromagnet, for instance, the positive interaction between nearest neighbors will incentivize each spin to align with its closest neighbors. An Ising machine will tend to find the spin configuration that minimizes the total energy of the spin network. This solution can then be translated into the solution of other optimization problem.
Heuristic Ising machines, like the one developed by the MIT team, only yields a candidate solution to the problem (which is, on average, close to the optimal solution). However, algorithms that always find the exact solution to the problem are difficult to apply to large problem sizes, as they would often have to run for hours, if not days, to terminate. Therefore, heuristic algorithms are an alternative to exact algorithms, since they provide fast and cheap solutions to hard problems.